9. KNN (K-Nearest Neighbors)

9.1 What are the basic concepts/ What problem does it solve?

KNN (K-nearest neighbors) attempts to estimate the conditional distribution of Y given X, and then classify agiven observation to the class with highest estimated probability.

9.2 What are the assumptions? What is the process of the algorithm? What is the cost function?

Given a positive integer $K$ and a test observation $x_0$, the KNN classifier first identifies the neighbors $K$ points in the training data that are closest to $x_0$, represented by $N_0$.

It then estimates the conditional probability for class $j$ as the fraction of points in $N_0$ whose response values equal $j$: $$ Pr(Y = j\vert X = x_0) = \frac{1}{K}\sum_{i \in N_0} I(y_i = j)$$.

Finally, KNN applies Bayes rule and classifies the test observation $x_0$ to the class with the largest probability.

9.5 What are the advantages and disadvantages?

Advantages:

• Easy to interpret output

• Naturally handles multi-class cases

• Predictive power, can do well in practice with enough representative data

Disadvantages:

• Large search problem to find nearest neighbors

• The choice of K has a drastic effect on the KNN classifier

10. Decision Tree

10.1 What are the basic concepts/ What problem does it solve?

Decision trees can be applied to both regression and classification problems.

These involve stratifying or segmenting the predictor space into a number of simple regions, we typically use the mean or the mode of the training observations in the region to which it belongs to make a prediction.

Decision Tree gets the name “tree” since the set of splitting rules used to segment the predictor space can be summarized in a tree.

• terminal nodes/leaves: the regions $R_1, R_2, \cdots, R_J$

• internal nodes: the points along the tree where the predictor space is split

• branches: the segments of the trees that connect the nodes

10.2 What is the process of the algorithm?

10.2.1 Regression Tree

1. Select the predictor $X_j$ and the cutpoint $s$ such that splitting the predictor space into the regions $\{X \vert X_j < s\}$ and $\{X \vert X_j \ge s \}$ leads to the greatest possible reduction in RSS.

2. For any $j$ and $s$, we define the pair of half-planes

$R_1(j, s) = \{X \vert X_j < s\}$ and $R_2(j, s) = \{X \vert X_j \ge s \}$,

and we seek the value of $j$ and $s$ that minimize the equation:

$$\sum_{i:x_i\in R_1(j,s)} (y_i-\hat{y_{R_1}})^2+ \sum_{i:x_i\in R_2(j,s)} (y_i-\hat{y_{R_2}})^2$$

where $\hat{y_{R_1}}$ is the mean response for the training observations in $R_1(j, s)$, $\hat{y_{R_2}}$ is the mean response for the training observations in $R_2(j, s)$.

Finding the values of j and s can be done quite quickly, especially when the number of features $p$ is not too large.

1. Instead of splitting the entire predictor space, we split one of the two previously identified regions

2. Repeat the process, looking for the best predictor and best cutpoint in order to split the data further so as to minimize the RSS.

3. The process continues until a stopping criterion is reached; for instance, we may continue until no region contains more than five observations.

10.2.2 Classfication Tree

1. Select the predictor $X_j$ and the cutpoint $s$ such that splitting the predictor space into the regions $\{X \vert X_j < s\}$ and $\{X \vert X_j \ge s \}$ leads to the greatest possible reduction in Classification Error Rate:

$$E= 1- \max_k (\hat{p}_{mk})$$

Here $\hat{p}_{mk}$ represents the proportion of training observations in the $m^{th}$ region that are from the kth class

1. Two other preferred measures instead of classification error are Gini Index and Cross-Entropy

Gini index: $G= \sum_{k=1}^K \hat{p}_{mk}(1- \hat{p}_{mk})$

Cross-Entropy: $D= -\sum_{k=1}^K \hat{p}_{mk} \log{\hat{p}_{mk}}$

1. Repeat this process, look for the best predictor and best cutpoint in order to split the data further so as to minimize the Classification Error Rate/Misclassification Rate within each of the resulting regions.

2. The process continues until a stopping criterion is reached.

10.2.3 Recursive binary splitting

• A top-down, greedy approach that is known as recursive binary splitting.

• It is top-down because it begins at the top of the tree (at which point all observations belong to a single region) and then successively splits the predictor space; each split is indicated via two new branches further down on the tree.

• It is greedy because at each step of the tree-building process, the best split is made at that particular step, rather than looking ahead and picking a split that will lead to a better tree in some future step.

10.3 What is the cost function?

Regression Tree: $$RSS:= \sum_{j=1}^J \sum_{i\in R_j}(y_i− \hat{y_{R_j}})^2$$

Classification Tree: Classification error rate: $E= 1- \max_k (\hat{p}_{mk})$

Gini index: $G= \sum_{k=1}^K \hat{p}_{mk}(1- \hat{p}_{mk})$

Cross-Entropy: $D= -\sum_{k=1}^K \hat{p}_{mk} \log{\hat{p}_{mk}}$

10.4 What are the and disadvantages?

Advantages:

• Trees are very easy to explain to people. In fact, they are even easier to explain than linear regression!

• More closely mirror human decision-making than the regression and classification approaches.

• Canbe displayed graphically, and are easily interpreted even by a non-expert.

• Easily handle qualitative predictors without the need to create dummy variables.

Disadvantages:

• Do not have the same level of predictive accuracy as some of the other regression and classification approaches.

• Calculations can get very complex, particularly if many values are uncertain or many outcomes are linked.

10.5 Tree Pruning

A large or complex tree is likely to overfit the data, leading to poor test set performance.

However, a smaller tree with fewer splits might lead to lower variance and better interpretation at the cost of a little bias.

One way to avoid overfit in smaller trees is to build the tree only so long as the decrease in the RSS due to each split exceeds some (high) threshold. A better strategy is to grow a very large tree $T_0$, and then prune it back in order to obtain a subtree.

Cost complexity pruning is a method to select a small set of subtrees instead of estimating test error using cross-validation or the validation set approach for every possible subtree.

Rather than considering every possible subtree, we consider a sequence of trees indexed by a nonnegative tuning parameter $\alpha$. For each value of $\alpha$ there corresponds a subtree $T \subset T_0$ such that

$$\sum_{m=1}^{\vert T \vert} \sum_{i: x_i \in R_m} (y_i-\hat{y_{R_m}})^2+ \alpha \vert T\vert$$

is as small as possible. Here $\vert T \vert$ indicates the number of terminal nodes of the tree $T$, $R_m$ is the rectangle (i.e. the subset of predictor space) corresponding to the $m^{th}$ terminal node, and $\hat{y_{R_m}}$ is the predicted response associated with $R_m$.

When $\alpha = 0$, then the subtree $T$ will simply equal $T_0$. As $\alpha$ increases, the above equation will tend to be minimized because there is a price to pay for having a tree with many terminal nodes.

• Summarize the algorithm as below:

1. Use recursive binary splitting to grow a large tree on the training data, stopping only when each terminal node has fewer than some minimum number of observations.

2. Apply cost complexity pruning to the large tree in order to obtain a sequence of best subtrees, as a function of $\alpha$.

3. Use K-fold cross-validation to choose $\alpha$. That is, divide the training observations into $K$ folds. For each $k= 1, . . .,K:$
     (a) Repeat Steps 1 and 2 on all but the kth fold of the training data.
     (b) Evaluate the mean squared prediction error on the data in the left-out $k^{th}$ fold, as a function of $\alpha$.
     Average the results for each value of $\alpha$, and pick α to minimize the average error.

4. Return the subtree from Step 2 that corresponds to the chosen value of $\alpha$.

11. Random Forest

11.1 What are the basic concepts/ What problem does it solve?

Random Forest is an ensemble learning method for classification, regression and other tasks, that operate by constructing a multitude of decision trees at training time and outputing the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees.

11.2 What is the process of the algorithm?

Randm Forest applys bagging to the decision tree:

• Bagging: random sampling with replacement from the original set to generate additional training data, the purpose of bagging is to reduce the variance while retaining the bias, it is effective because you are improving the accuracy of a single model by using multiple copies of it trained on different sets of data, but bagging is not recommended on models that have a high bias.
• Randomly selection of m predictions: used in each split, we use a rule of thumb to determine the number of features selected $m=\sqrt{p}$, this process decorrelates the trees.
• Each tree is grown to the largest extent possible and there is no pruning.
• Predict new data by aggregating the predictions of the ntree trees (majority votes for classification, average for regression).

11.3 What is the cost function?

Same as Decision Tree

11.5 What are the advantages and disadvantages?

Advantages:

• The process of averaging or combining the results of different decision trees helps to overcome the problem of overfitting.

• It outperforms a single decision tree in terms of variance when using for a large data set.

• Random forest is extremely flexible and have very high accuracy.

• It also maintains accuracy even when there are a lot of missing data.

Disadvantages:

• It is much harder and time-consuming to construct the tress and implement the prediction process than decision trees.

• It also requires more computational resources and less intuitive. When you have a large collection of decision trees it is hard to have an intuitive grasp of the relationship existing in the input data.

12. Boosting

12.1 What are the basic concepts/ What problem does it solve?

Boosting is general approach for improving the predictions resulting, which can be applied to many statistical learning methods for regression or classification, especially for decision trees.

The main idea of boosting is to add new models to the ensemble sequentially: each tree is grown using information from previously grown trees. Boosting does not involve bootstrap sampling; instead each tree is fit on a modified version of the original data set. At each particular iteration, a new weak, base-learner model is trained with respect to the error of the whole ensemble learnt so far.

12.2 What is the process of the algorithm?

Consider first the regression setting, boosting involves combining a large number of decision trees, $\hat{f^1}, \hat{f^2}, \dots, \hat{f^B}$, boosting is described as below.

1. Set $\hat{f}(x)=0$ and $r_i= y_i$ for all $i$ in the training set.

2. For $b = 1, 2, \dots, B$, repeat:
     (a) Fit a tree $\hat{f^b}$ with $d$ splits ($d+1$ terminal nodes) to the training data $(X, r)$.
     (b) Update $\hat{f}$ by adding in a shrunken version of the new tree: $\hat{f}(x)\gets \hat{f}(x)+ \lambda \hat{f^b}(x)$
     (c) Update the residuals, $r_i \gets r_i- \lambda \hat{f^b}(x_i)$
   

3. Output the boosted model, $$\hat{f}(x)= \sum_{b=1}^B \lambda \hat{f^b}(x)$$

Note: in boosting, unlike in bagging, the construction of each tree depends strongly on the trees that have already been grown.

Boosting classification trees proceeds in a similar but slightly more complex way, it has three tuning parameters:

• The number of trees $B$. Boosting can overfit if $B$ is too large, although this overfitting tends to occur slowly if at all. We use cross-validation to select $B$.
• The shrinkage parameter $\lambda$, a small positive number. This controls the rate at which boosting learns. Typical values are 0.01 or 0.001, and the right choice can depend on the problem. Very small $\lambda$ can require using a very large value of $B$ in order to achieve good performance.
• The number $d$ of splits in each tree, which controls the complexity of the boosted ensemble. More generally $d$ is the interaction depth, and controls the interaction order of the boosted model, since $d$ splits can involve depth at most $d$ variables.

12.4 What is the cost function?

It depends on the model, could be square loss or exponential loss. For any loss function, we can derive a gradient boosting algorithm. Absolute loss and Huber loss are more robust to outliers than square loss.

12.5 What are the advantages and disadvantages?

Advantages:

• Although Boosting can overfit fit with higher number of trees, it generally gives somewhat better results than Random Forests if the three parameters are correctly tuned.

• Often provides predictive accuracy that cannot be beat.

• It can optimize on different loss functions and provides several hyperparameter tunning options that make the function fit very flexible.

• No data preprocessing required and can handles missing data.

Disadvantages:

• Boosting can overemphasize outliers and cause overfitting, we must use cross-validation to neuralize.

• Boosting often requires many trees (>1000) which can be time and memory exhaustive.

• The high flexibility results in many parameters that interact and influence heavily the behavior of the approach. This requires a large grid search during tunning.

• Less interpretable although this is easily addressed with various tools (varaible importance, partial dependence plots, LIME, etc.)

13. Neural Network

13.1. What are the basic concepts/ What problem does it solve?

Neural Network is an algorithm that try to mimic the brain, where many simple units, called neurons, are interconnected by weighted links into larger structures of remarkably high performance. It was very widely used in 80s and early 90s; popularity diminished in late 90s.

A neural network is nonlinear statistical, two-stage model applies both to regression or classification.

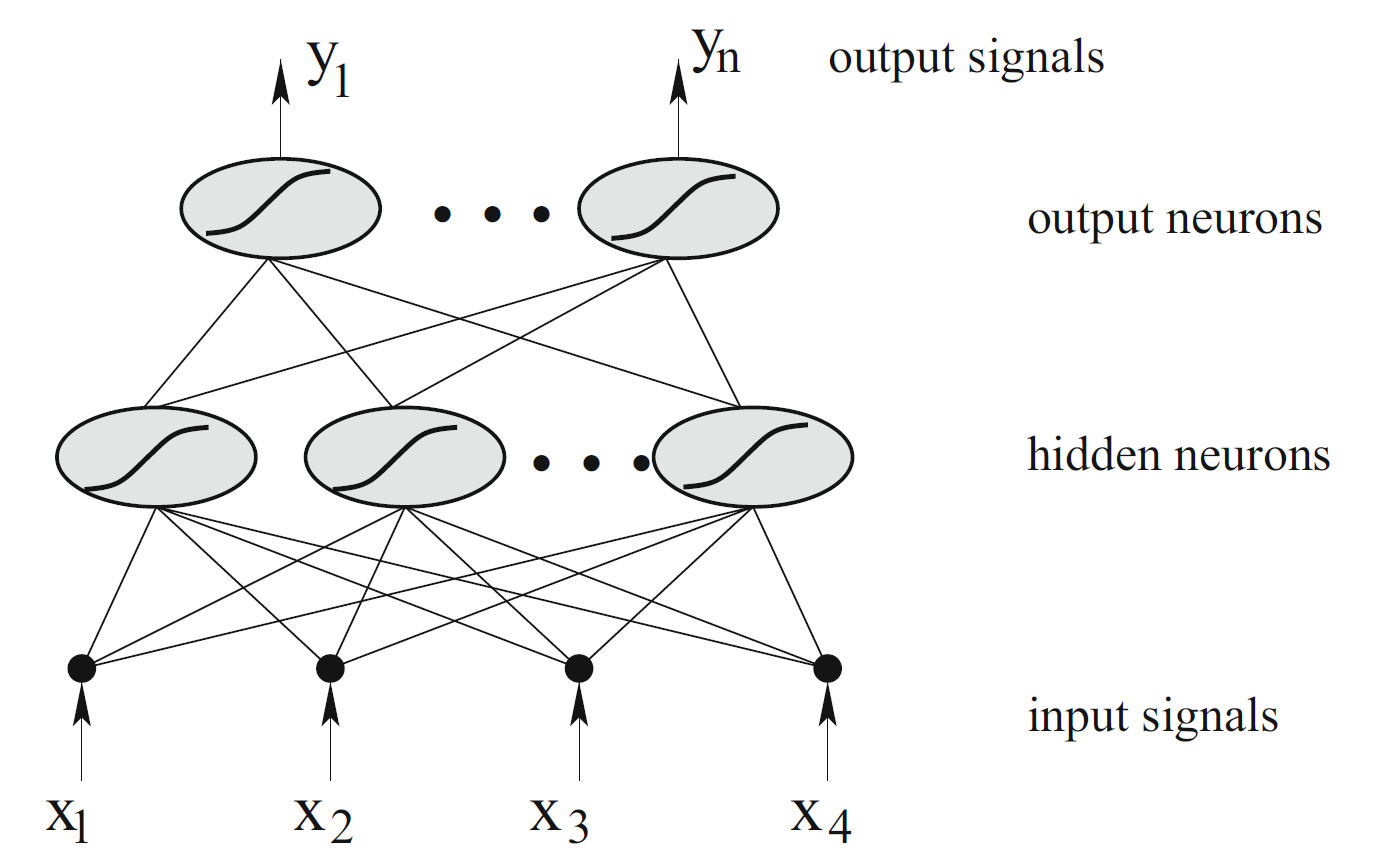
An example neural network consisting of two interconnected layers - An Introduction to Machine Learning

For K-class classification, there are $K$ units at the top, with the $k^{th}$ unit modeling the probability of class k. There are $K$ target measurements $Y_k, k = 1, \dots, K$, each being coded as a 0-1 variable for the $k^{th}$ class.

Hidden Units $Z_m$ are created from linear combinations of the inputs: $$Z_m= \sigma(\alpha_{0m}+\alpha_m^T X), Z= (Z_1, Z_2, \dots, Z_M)$$

And then the target $Y_k$ is modeled as a function of linear combinations of the $Z_m$
$T_k = \beta_{0k}+ \beta_k^T Z, k= 1, \dots, K$
$f_k(X) = g_k(T)$, $k= 1, \dots, K$
where $Z = (Z_1, Z_2, \dots, Z_M)$, and $T = (T_1, T_2, \dots, T_K)$.

The activation function $\sigma(v)$ is usually chosen to be the sigmoid $\sigma(v) = 1/(1+e^{-v})$. Sometimes Gaussian radial basis functions are used.

Weights and Biases between each layer W and b, weights tell you what kind of pattern this neuron in the second layer is picking up on;

13.2 What is the process of the algorithm?

13.2.1 Training a neural network

Pick a network architecture (connectivity pattern between neurons)

• No. of input units: Dimension of features
• No. output units: Number of classes
• Reasonable default: 1 hidden layer, or if >1 hidden layer, have same no. of hidden units in every layer (usually the more the better)

1. Randomly initialize weights

2. Implement forward propagation to get $h_{\Theta}(x^{(i)})$ for any $x^{(i)}$

3. Implement code to compute cost function $J(\Theta)$

4. Implement backprop to compute partial derivatives $\frac{\partial}{\partial \Theta_{jk}^{(l)}} J(\Theta)$
     for i = 1:m
      Perform forward propagation and backpropagation using example $(x^{(i)}, y^{(i)})$
   (Get activations $a^{(l)}$ and delta terms $\delta^{(l)}$ for $l= 1,2,\dots, L$.)

5. Use gradient checking to compare $\frac{\partial}{\partial \Theta_{jk}^{(l)}} J(\Theta)$ computed using backpropagation vs. using numerical estimate of gradient of $J(\Theta)$.
   Then disable gradient checking code.

6. Use gradient descent or advanced optimization method with backpropagation to try to minimize $J(\Theta)$ as a function of parameters $\Theta$

13.2.1 Backpropagation

Intuition: $\delta_j^{(l)}=$ “error” of node $j$ in layer $l$.

Backpropagation algorithm:

Training set $\{(x^{(1)}, y^{(1)}), \dots, (x^{(m)}, y^{(m)}) \}$

Set $\Delta_{ij}^{(l)}= 0$ (for all $l, i, j$).

For $i=1$ to $m$
  Set $a^{(1)}= x^{(i)}$
  Perform forward propagation to compute $a^{(l)}$ for $l= 1,2,\dots, L$
  Using $y^{(i)}$, compute $\delta^{(L)}= a^{(L)}- y^{(i)}$
  Compute $\delta^{(L-1)}, \delta^{(L-2)}, \dots, \delta^{(2)}$
  $\Delta_{ij}^{(l)}:= \Delta_{ij}^{(l)}+ a_{j}^{(l)} \delta_{i}^{(l+1)}$

$D_{ij}^{(l)}:= \frac{1}{m} \Delta_{ij}^{(l)}+ \lambda \Theta{ij}^{(l)}$ if $j\neq 0$

$D_{ij}^{(l)}:= \frac{1}{m} \Delta_{ij}^{(l)}$ if $j= 0$
where, $\frac{\partial}{\partial \Theta_{jk}^{(l)}} J(\Theta)= D_{ij}^{(l)}$

13.3 What is the cost function?

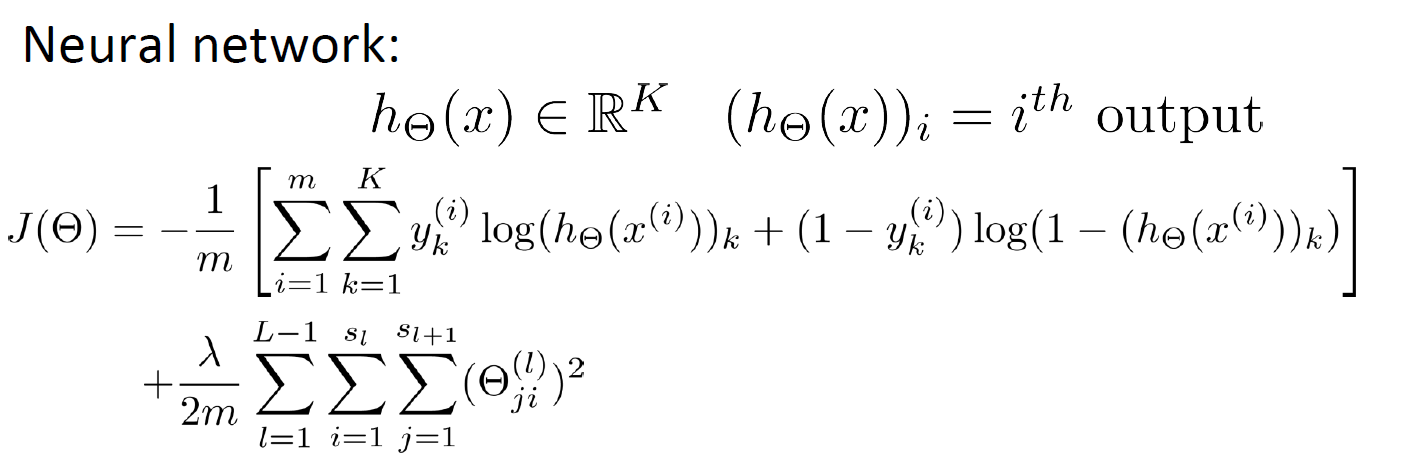
13.4 What are the advantages and disadvantages?

Advantages:

• Neural Network is able to learn and model non-linear and complex relationships in real-life data, which many of the relationships between inputs and outputs are non-linear as well as complex.

• NNs can establish the model, generalize and predict on unseen data.

• Unlike many other prediction techniques, ANN does not impose any restrictions on the input variables (like how they should be distributed). Additionally, many studies have shown that ANNs can better model heteroskedasticity i.e. data with high volatility and non-constant variance, given its ability to learn hidden relationships in teh data without imposing any fixed relationships in the data. This is something very useful in financial time series forcasting where data volatility is very high.

• Significantly outperform other models when the conditions are right (lots of high quality labeled data).

Disadvantages:

• Hard to interpret the model because NNs are a black box model once they are trained.

• Not work well on small data sets, where he Bayesian approaches do have an advantage here.

• Hard to tune to ensure they learn well, and therefore hard to debug.

• ANNs are computationally-expensive and time-consuming to train on very large datasets.

14. K-means Clustering

14.1 What are the basic concepts/ What problem does it solve?

K-means clustering is a well-known, simple and elegant clustering method, approach for partitioning a data set into $K$ distinct, non-overlapping clusters. To perform K-means clustering, we must first specify the desired number of clusters K; then the K-means algorithm will assign each observation to exactly one of the K clusters.

Clustering refers to a very broad set of techniques for finding homogeneous subgroups, or clusters among the observations.

14.2 What are the assumptions?

Data has to be numeric, not categorical.

Let $C_1, \dots, C_K$ denote sets containing the indices of the observations in each cluster. These sets satisfy two properties:

1. $C1 \cup C2 \cup \dots \cup C_K = \{1,\dots,n \}$. In other words, each observation belongs to at least one of the $K$ clusters.
2. $C_k \cap C_{k'} = \emptyset$ for all $k \neq k'$. In other words, the clusters are nonoverlapping: no observation belongs to more than one cluster.

14.3 What is the process of the algorithm?

1. Randomly assign a number, from 1 to K, to each of the observations.
   These serve as initial cluster assignments for the observations.

2. Iterate until the cluster assignments stop changing:
   (a) For each of the K clusters, compute the cluster centroid. The $k^{th}$ cluster centroid is the vector of the $p$ feature means for the observations in the $k^{th}$ cluster.
   (b) Assign each observation to the cluster whose centroid is closest (where closest is defined using Euclidean distance).

14.4 What is the cost function?

• We want to partition the observations into $K$ clusters such that the total within-cluster variation, summed over all $K$ clusters, is as small as possible. That is, we want to solve the problem:
  $$\min_{C_1,\dots,C_K}\sum_{k=1}^K W(C_k)$$.

• Define the within-cluster variation, involving squared Euclidean distance: $$W(C_k)= \frac{1}{\vert C_k\vert} \sum_{i,i’ \in C_k} \sum_{j=1}^p (x_{ij}-x_{i’j})^2$$.

where $\vert Ck\vert$ denotes the number of observations in the $k^{th}$ cluster. In other words, the within-cluster variation for the $k^{th}$ cluster is the sum of all of the pairwise squared Euclidean distances between the observations in the $k^{th}$ cluster, divided by the total number of observations in the $k^{th}$ cluster.

• Combining above two formulas, we give the optimization problem that defines K-means clustering: $$\min_{C_1,\dots,C_K}\sum_{k=1}^K \frac{1}{\vert C_k\vert}\sum_{i,i’\in C_k}\sum_{j=1}^p (x_{ij}-x_{i’j})^2 $$

14.5 What are the advantages and disadvantages?

Advantages:

• Easy to implement and easy to interpret the clustering results.

• K-means is fast and efficient, in terms of computational cost.

Disadvantages:

• Sensitive to outliers

• Initial centroids are randomly selected and have a strong impact on the final results.

• K-the number of clusters are not known, it’s sometimes difficult to choose the best number.

• Scaling your datasets or not (normalization or standardization) will completely change results.

• It does not work well with clusters (in the original data) of different size and different density.

15. SVM (Support Vector Machine)

15.1 What are the basic concepts/ What problem does it solve?

SVM constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks like outliers detection. It is an alternative view of logistic regression.

One reasonable choice as the best hyperplane is the one that represents the largest separation, or margin, between the two classes. So we choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. If such a hyperplane exists, it is known as the maximum-margin hyperplane and the linear classifier it defines is known as a maximum-margin classifier.

15.2 What is the process of the algorithm?/ What is the cost function?

Hard-margin (the training data is linearly separable):

With a normalized or standardized dataset, these hyperplanes can be described by the equations:

$\vec{w} \cdot \vec{x}- b= 1$ (anything on or above this boundary is of one class, with label 1)
and
$\vec{w} \cdot \vec{x}- b= -1$ (anything on or below this boundary is of the other class, with label −1).

Geometrically, the distance between these two hyperplanes is $\frac{2}{\vert\vert \vec{w} \vert\vert}$, so to maximize the distance between the planes we want to minimize $\vert\vert \vec{w} \vert\vert$. The distance is computed using the distance from a point to a plane equation. We also have to prevent data points from falling into the margin, we add the following constraint: for each $i$ either

$\vec{w} \cdot \vec{x_i}- b \ge 1$, if $y_i= 1$
or
$\vec{w} \cdot \vec{x_i}- b \le 1$, if $y_i= -1$

These constraints state that each data point must lie on the correct side of the margin.

This can be rewritten as

$y_i(\vec{w} \cdot \vec{x_i}- b) \ge 1$, for all $1\ne i \ne n$

We can put this together to get the optimization problem:

Minimize $\vert\vert \vec{w} \vert\vert$ subject to $y_i(\vec{w} \cdot \vec{x_i}- b) \ge 1$, for all $1\ne i \ne n$

The $\vec{w}$ and $b$ that solve this problem determine our classifier, $\vec{x} \mapsto sgn(\vec{w} \cdot \vec{x_i}- b)$

Soft-margin (the data are not linearly separable) The hinge loss function: $$\max (0, 1-y_i(\vec{w} \cdot \vec{x_i}- b))$<br> Note that$y_i$is the i-th target and$\vec{w} \cdot \vec{x_i}- b$$ is the current output.

We then wish to minimize $$\frac{1}{n} \sum_{i=1}^n \max(0, 1-y_i(\vec{w} \cdot \vec{x_i}- b)) + \lambda {\vert\vert \vec{w} \vert\vert }^2$where the parameter$\lambda$determines the trade-off between increasing the margin size and ensuring that the$\vec{x_i}$lie on the correct side of the margin. Thus, for sufficiently small values of$\lambda$$, the second term in the loss function will become negligible, hence, it will behave similar to the hard-margin SVM, if the input data are linearly classifiable, but will still learn if a classification rule is viable or not.

Kernel (Non-Linear Decision Boundary):

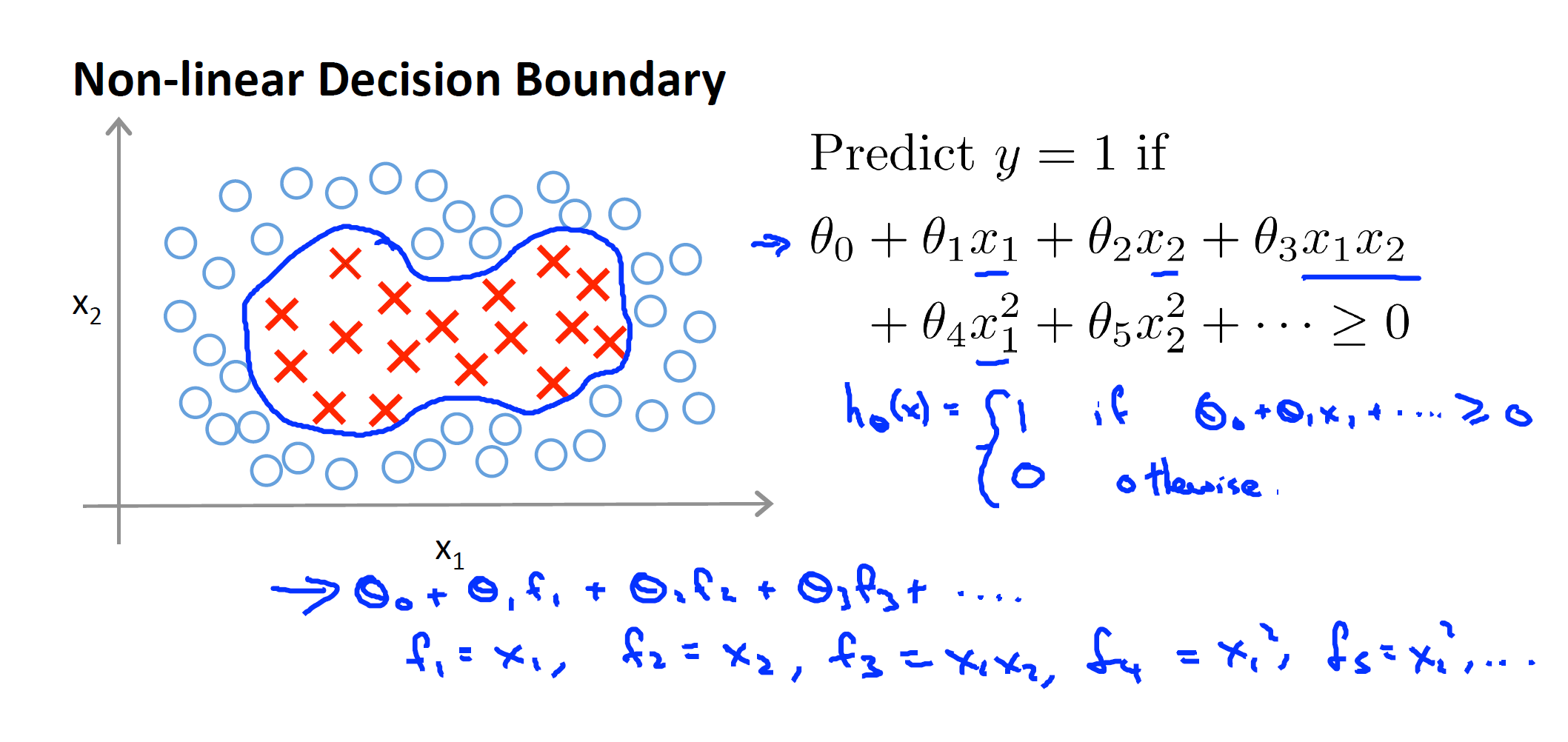
15.3 What are the advantages and disadvantages?

Advantages:

• SVM models have generalization in practice, the risk of overfitting is less in SVM.
• The kernel trick is real strength of SVM, that is, we can solve complex problem with an appropriate kernel function.
• An SVM is defined by a convex optimization problem (no local minima)
• Works well with even unstructured and semi-structured data and high-dimensional data.

Disadvantages:

• Choose a “good” kernel function is not easy.
• Long training time for large datasets.
• Difficult to understand and interpret the final model, varaible weights and individual impact.
• In p > n cases, SVM works poorly.

16. PCA (Principal Component Analysis)

16.1. What are the basic concepts/ What problem does it solve?

PCA is an unsupervised approach, since it involves only a set of features $X_1,X_2,\dots, X_p$, and no associated response $Y$ . Apart from producing derived variables for use in supervised learning problems.

PCA also serves as a tool for data visualization (visualization of the observations or visualization of the variables).

PCA provides a tool to find a low-dimensional representation of a data set that contains as much as possible of the variation. The idea is that each of the $n$ observations lives in p-dimensional space, but not all of these dimensions are equally interesting.

PCA seeks a small number of dimensions that are as interesting as possible, where the concept of interesting is measured by the amount that the observations vary along each dimension. Each of the dimensions found by PCA is a linear combination of the p features.

16.2 What are the assumptions?

• Data should be large enough and be suitable for data reduction.

• No significant outliers. Outliers are important because these can have a disproportionate influence on your results.

16.3 What is the process of the algorithm?

1. Given a $n \times p$ data set $X$, center each variable in $X$ to have mean zero (that is, the column means of X are zero).

2. Look for the linear combination of the sample feature values of the form:
        $z_{i1}= \phi_{11}x_{i1}+ \phi_{21} x_{i2}+ \cdots+ \phi_{p1} x_{ip}$
   that has largest sample variance, subject to the constraint that $\sum_{j=1}^p \phi_{j1}^2= 1$.
   In other words, the first principal component loading vector solves the optimization problem
        $\max_{\phi_{11},\cdots,\phi_{p1}} \frac{1}{n} \sum_{i=1}^n(\sum_{j=1}^p \phi_{j1} x_{ij}) s.t. \sum_{j=1}^p \phi_{j1}^2= 1$
   We refer to $z_{11}, \dots, z_{n1}$ as the scores of the first principal component.

3. After the first principal component $Z_1$ of the features has been determined, we can find the second principal component Z2. The second principal component is the linear combination of $X_1, \dots, X_p$ that has maximal variance out of all linear combinations that are uncorrelated with $Z_1$.
   The second principal component scores $z_{12}, z_{22}, \dots, z_{n2}$ take the form
        $z_{i2}= \phi_{12}x_{i1}+ \phi_{22}x_{i2}+\cdots+\phi_{p2}x_{ip}$
   where $\phi_2$ is the second principal component loading vector, with elements $\phi_{12}, \phi_{22}, \dots, \phi_{p2}$. It turns out that constraining $Z_2$ to be uncorrelated with $Z_1$ is equivalent to constraining the direction $\phi_{1}$ to be orthogonal (perpendicular) to the direction $\phi_{1}$.

4. In a larger data set with $p > 2$ variables, there are multiple distinct principal components, and they are defined in a similar manner.

5. Once we have computed the principal components, we can plot them against each other in order to produce low-dimensional views of the data. For instance, we can plot the score vector $Z_1$ against $Z_2$, $Z_1$ against $Z_3$, $Z_2$ against $Z_3$, and so forth. Geometrically, this amounts to projecting the original data down onto the subspace spanned by $\phi_1, \phi_2$, and $\phi_3$, and plotting the projected points.

16.4 What are the advantages and disadvantages?

Advantages:

• Reflects the intuition about the data.

• Allows estimating probabilities in high-dimensional data, no need to assume independence.

• Perform variable reduction, lead to faster processing and smaller storage.

Disadvantages:

• Too expensive for many applications.

• The variance of each column can make big difference to the result, be sure to normalize the data at first.